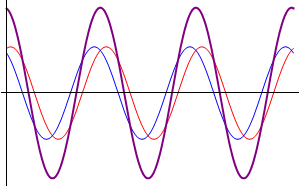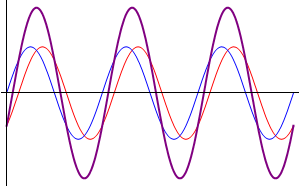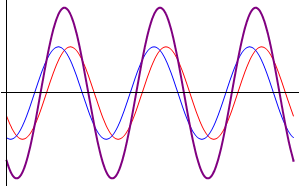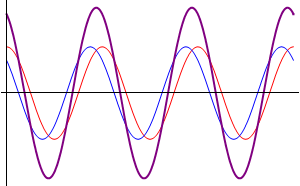
Ondas Física 2: Superposicion de ondas

Esto sucede cuando dos o mas ondas se mueven por el mismo medio y la onda resultante es la suma algebraica de las ondas individuales.

Teniendo como ejemplo uno de los casos mas simples: Son dos ondas que se propagan en una misma cuerda con la misma direccion, frecuencia y amplitud solo con la unica diferencia de su desfase, esto se podria escribir como:

$y_1 = A_0\cos(\omega t - k x)\,$ $y_2 = A_0\cos(\omega t - k x+\phi)\,$

Esta superposicion de onda se convertiria en :

$y = 2A_0\cos\left(\frac{\phi}{2}\right)\cos\left(\omega t - k x+\frac{\phi}{2}\right) = A(\phi)\cos\left(\omega t - k x+\phi'\right)$
Con:

$A(\phi) = 2A_0\cos\left(\frac{\phi}{2}\right)\qquad\qquad\phi'=\frac{\phi}{2}$
Esto quiere decir que se tienen dos ondas en el mismo sentido, frecuencia y amplitud en una nueva onda con un desfase que es la media de las ondas individuales y la amplitud de la resultante depende de su desfase.
Ahora gracias al desfase tenemos dos casos muy importantes:

Interferencia constructiva:Esto sucede cuando el desfase entre cada onda es un multiplo par de $π$ , o hablando de la distancia entre máximos de las ondas, si están desfasados en un número entero de longitudes de onda

$\phi = 2n\pi\,$ $\Rightarrow$ $\Delta x = n\lambda\,$
En estos casos las ondas coinciden y la onda resultante se hace una en fase con ellas y respecto a la amplitud se hace doble de la de cada una.

$A(0) = 2A_0\qquad\phi'(0)=0$

Interferencia destructiva: Esto sucede cuando el desfase entre cada onda es un multiplo impar de $π$ , o hablando de la longitud, cuando se diferencian en un múltiplo semientero de la longitud de onda (media longitud de onda, longitud y media, dos longitudes y media,…)

$\phi = (2n+1)\pi\,$ $\Rightarrow$ $\Delta x = n\lambda\,$ Si las ondas se encuentran en una contrafase las ondas se convierten exactamente iguales pero con la diferencia que van con el signo contrario, esto hace que se cancelen mutuamente y esto provocara un resultado de una onda nula (interferencia destructiva).

$A(\pi) = 0 \qquad \phi'=\frac{\pi}{2}$
Si superponemos unas ondas senoidales que tengan la misma frecuancia pero con distintas amplitudes y/o fases de resultado se obtendra otra onda senoidal con la misma frecuencia, pero con diferentes amplitudes y/o fases. Las ondas se podrian cancelar si llegaran a tener la misma amplitud y con una diferencia de la fase de 180°.

Ondas Física 2

miércoles, 23 de noviembre de 2016

Superposicion de ondas

No hay comentarios:

Publicar un comentario